Welcome back to the Unfinished Learning in Middle School Math series, in which math educators Chrissy Allison and Becca Varon illustrate how to make some of the trickiest standards in grades 6-8 accessible for all students. Over the course of six blog posts, we’ll provide concrete examples of how math educators can address unfinished learning within the context of grade-level lessons, which in the long term will help prevent an entrenched pattern of over-remediation and below-grade-level teaching. You can read our introductory post here. In this fourth post, we will explore ways to “bridge the gap” with the 7th-grade standard 7.NS.A.3.
Let’s take a look at the standard itself. As you read, consider how it applies to your everyday life.
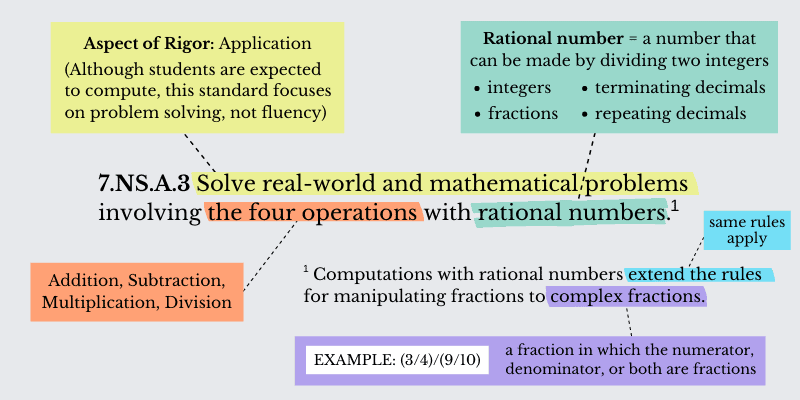
| 7.NS.A.3: Solve real-world and mathematical problems involving the four operations with rational numbers. Computations with rational numbers extend the rules for manipulating fractions to complex fractions. |
Did anyone else almost have a heart attack when thinking about teaching this standard to middle schoolers with significant unfinished learning? We know we did!
In fact, years ago, when we started digging deeper into the topic of unfinished learning, 7.NS.A.3 was the standard that popped into my head because it relies heavily on skills and understanding from previous grade levels.
Let’s take a moment to study and understand this standard:
Here’s the truth: We’d love students to have a deep understanding of every standard, and it’s important to work toward that every day in our classrooms. That said, there are some standards that have bigger implications for future learning and are a greater necessity for our everyday lives— and this is the case for standard 7.NS.A.3.
We absolutely need this standard for life. It’s non-negotiable whether you’re creating a budget, managing your finances, or cooking a meal for your family—not to mention starting a business or moving into higher study of math. Engaging in common, everyday experiences involving operations with integers, fractions, and decimals is essential for students as they move into adulthood. This comfort with the math that will enable students to thrive financially and personally is a gift that not all of us were given in school ourselves.
Take a look at these tasks from Illustrative Mathematics. You’ll see the breadth of skills encompassed as part of 7.NS.A.3:
After analyzing and solving several problems aligned to this culminating standard, we’ll admit we felt a bit overwhelmed thinking about the prerequisites from K-6 that are embedded in the work of 7.NS.A.3.
Is your heart beating faster yet? Wondering if you need to reteach the entirety of the K-6 standards for students to be successful with 7.NS.A.3?
The short answer is no. This is not the time or place to start back at square one teaching students to add, subtract, multiply, and divide whole numbers, fractions, and decimals. You don’t have enough instructional time, nor is that the main goal of this standard. (Whew!)
Okay, so if fluency with the operations isn’t the focus, then what is?
Let’s take a look at a problem from this 7th-grade lesson in the Illustrative Mathematics curriculum to shed some light.
When considering what it will take for students to engage in problem-solving and answering the questions correctly, three things come to mind:
1. Understanding the meaning of the problem. Familiarity with some of the vocabulary, such as “utility,” “kilowatt-hour,” “solar panel,” “credit,” and “charge,” will help students comprehend this real-life situation.
2. Planning a solution pathway. To answer each question, students must determine which calculations to perform, and with which numbers. They’ll need to recognize that subtraction makes sense for part 1, while division is called for in parts 2 and 3.
3. Calculating with positive and negative decimals. Finally, students will need to find the difference and quotients to answer this three-part question.
While all three of these parts are necessary to be successful with this task, it’s important to remember that the aspect of rigor for 7.NS.A.3 is application. That means that the top priority is problem-solving, which means providing students with the opportunity to make sense of problems and persevere in solving them (Standard for Mathematical Practice 1) — not drill and kill with integers, fractions, and decimals.
So, let’s say that you open your curriculum and see this problem on the docket for next week, but you’ve diagnosed that your students have some unfinished learning when it comes to understanding and performing operations.
Perhaps you’ve noticed students struggling to calculate fractions and decimals by hand in previous lessons, or maybe you have evidence from a formative or diagnostic assessment that students often apply an incorrect operation when problem-solving. Conceptual gaps have greater implications than skill-based gaps, so make sure you gauge students’ understanding, not just level of procedural fluency.
It’s natural to look at a rigorous problem and worry, “My kids can’t do that,” especially if you’ve put similar problems in front of students and it hasn’t gone well!
Over time, that negative reinforcement can lead teachers to a variety of responses that decrease students’ access to cognitively demanding, grade-level work. Those responses can include:
- Removing the problem from the lesson or not teaching it altogether
- Over-scaffolding the problem by walking students through it, step-by-step
- Adapting the problem to make it easier, perhaps by replacing fractions and decimals with whole numbers, without a plan to reach the standard’s full breadth later
What can you do to take action in a way that meets students where they are while keeping the rigor bar high and engaging students in deep thinking about math? Here are a few recommendations:
1. Bucket the critical prerequisites into two categories: skills, and concepts.
- Skills: identifying opposites, finding absolute value, operations with positive and negative integers, performing operations with whole numbers, fractions, decimals
- Concepts: opposites, integers, addition, subtraction, multiplication, division
2. To support students with the skills they need in the short term, allow use of a calculator.
- The focus of this standard is supporting students to be resourceful problem solvers, not human calculators. Spending days or weeks teaching “basic skills” is not a good use of your limited instructional time when it comes to teaching 7.NS.A.3.
- This statement is backed by the National Council of Teachers of Mathematics (NCTM)’s Principles to Actions report (2014), which lists as an unproductive belief: “Calculators and other tools are at best a frill or distraction and at worst a crutch that keeps students from learning mathematics. Students should use these tools only after they have learned how to do procedures with paper and pencil.” Instead, a productive belief is that technology is a powerful tool that can support conceptual understanding, mathematical reasoning, and problem-solving.
3. Build understanding of concepts and vocabulary through visual representations and class discussion.
- Take advantage of “teachable moments” as they come up in grade-level lessons. For example, with the Buying & Selling Power problem, you could show a short video clip to build background knowledge about solar energy. To reinforce the relationship between multiplication and division, you could draw a picture to represent the charge of $0.12 per kilowatt hour, and have students discuss why it makes sense to divide $82.04 by $0.12 to answer question 2.
- Incorporate Math Talks in your daily or weekly lessons as a way to build understanding of concepts and continue working toward fluency. Fawn Nguyen’s free Math Talks site includes a list of resources, tips from her experiences implementing math tasks in her own classroom, and links to Math Talks you can use with your own students.
Who is ready to think?
In conclusion, we must allow all students to be problem-solvers and have access to cognitively demanding tasks, even if they have unfinished learning with rational number operations. Though it might be counterintuitive, fluency with skills is not a prerequisite for having the opportunity to solve problems. The truth is that all students are ready to think.