Back in 2012, I had an idea for getting a bit better at teaching. Kids make a lot of mistakes while learning. Teachers, meanwhile, have to quickly respond to those mistakes. What if I could prepare for those moments outside of the classroom?
I started collecting interesting mistakes my students made — as a new teacher, I had a lot to choose from. I thought if I shared these mistakes online, teachers would discuss them and I could learn how best to respond in class. I started the website mathmistakes.org, and very quickly a group of us were having some very interesting conversations about the student work I posted.
A typical post would focus on a single mistake. I’d share a picture, and ask two questions:
- Why did the student make the mistake?
- How would you help this student?
Other teachers sent me their own snapshots of student work, and I soon compiled hundreds of mistakes on the site.
The Pitfalls of Discussing Mistakes
With time, I became dissatisfied with the discussions we were having on the site. Too often the conversation veered into vague generalizations — “kids always do that” — or people would swap teaching ideas in a confusing way.
Looking back, I made a number of my own mistakes in the way I framed those conversations.
First, I asked others to explain why students made their mistakes. This is a question that we rarely can answer with any certainty. Besides, from the perspective of a teacher, a mistake doesn’t need to be explained — it needs to be addressed, with teaching.
Second, I focused attention on an individual student and their errors. Far be it from me to say every individual doesn’t deserve attention. However, teachers almost never have the ability to address individual mistakes in class, one at a time. If students struggle with a question on some quiz or assessment, the most bang for our buck comes from responding to the entire class at once.
Finally, I focused exclusively on mistakes. Certainly, mistakes are interesting — no regrets there. At the same time, mistakes are only half the story. We rarely talked about how, though some students fall into error, others successfully make sense of those very problems.
Better Student Work Discussions
After many years, I started to understand how to avoid those pitfalls.
“I’m going to show you a student mistake,” I’d say to a group of teachers, either online or in-person. “It’s only one student, but let’s imagine that a lot of students had similar issues.” No longer do I ask us to think about responding to a single student.
After I share the mistake, I’ll ask teachers what they notice about the work.
It’s at this point that, in the past, I might have asked everyone to try to explain why students make this particular mistake. I now know to avoid this. Instead, I ask about the learning goals.
“Based on this work, what should we try to teach this student?” Sometimes, the answer is obvious. Other times, it takes a bit of digging. Take this piece of work, for example:
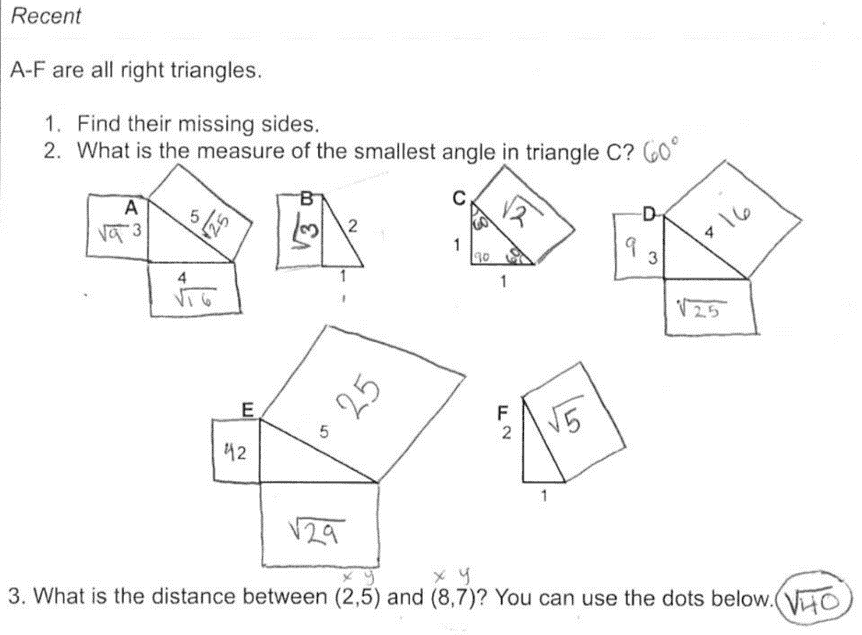
There is a great deal to notice here, from the sketching of squares to the correct calculation of distance. Clearly, this student knows a lot about the Pythagorean Theorem.
What they are not yet doing is distinguishing between cases where the hypotenuse is given and cases where it is the missing side. This student is treating those situations as the same — we should teach them the difference.
Customizing a Learning Activity
“Let’s try to create a worked example that could show students how to think correctly about this, along with a few practice problems,” I’ll then say.
Worked example activities are easy to customize. Making a great worked example activity is not necessarily easy, but it is a relatively simple format that many teachers can work with.
For my example, I chose to illustrate that the longest side of a triangle is always the “c” in a2+b2=c2. Along with the example, I wrote a pair of “self-explanation prompts,” to encourage students to think carefully about the work.
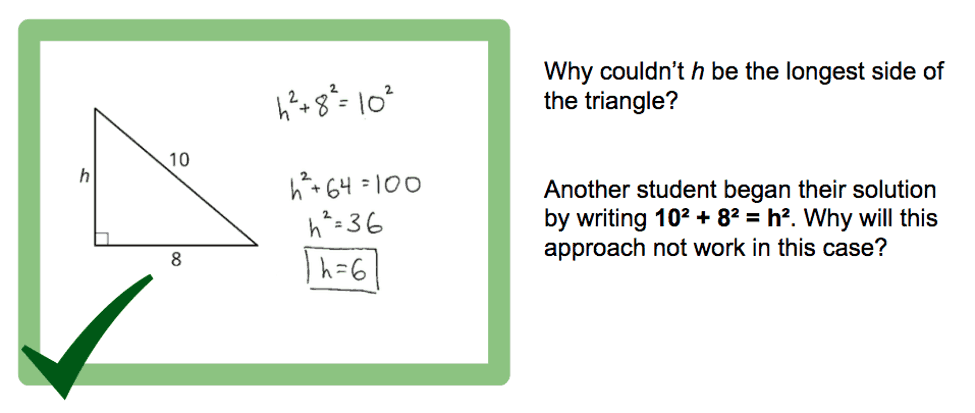
Research supports the idea that it’s good to follow-up worked examples with a few practice problems. Here are two problems I chose for this case:
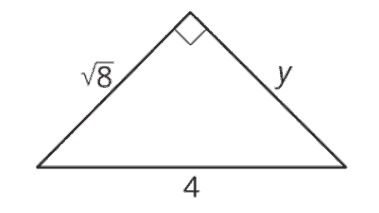
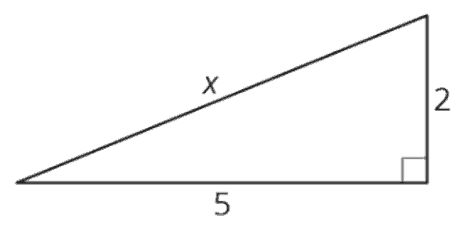
This is the end result of discussing student work. The discussion ends when we have a plan for helping students learn.
If we are to learn from studying mistakes, it is not enough to explain what went wrong in the learning or teaching process. Every error tells us what students are ready to learn. When we customize learning activities for these specific goals, we laser-focus our teaching on the needs of the class. Learning how to do this is the true power of discussing student work with others.














