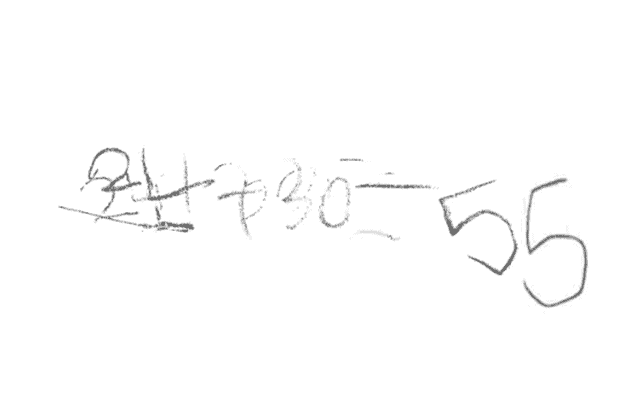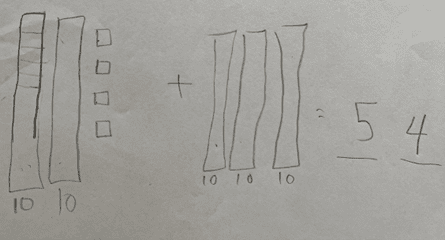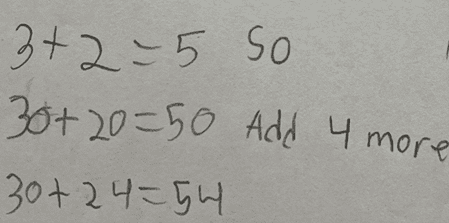What thoughts come to mind when you look at this example of student work?

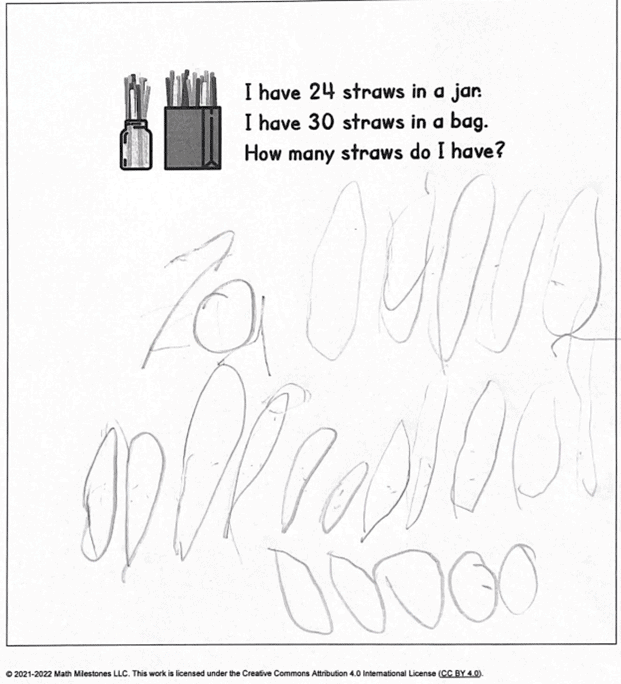
What do you notice? What are you wondering? If you collected this student’s work and looked at it later in the week, or even later that day, what would you learn about the ways in which the student engaged with the concepts?

As an English language supports specialist in an elementary school, I co-teach with classroom teachers to provide multilingual learners equitable access to grade-level content while advancing their social and academic English. Two questions I consistently ask myself when planning and facilitating learning experiences in mathematics are:

 “How can I offer students multiple avenues to reason through a task?”

“How can I be curious about student thinking in order to uncover what students already understand?”

A Second-Grade Example Using Math Milestones™

During the first week of the school year, the classroom teacher and I selected Math Milestones™ task 1:6 in order to uncover how students engaged with some of the critical concepts of addition and place value in grades K-2. The class is comprised of 23 students, 9 of whom are multilingual learners. These students speak Spanish, Korean, Indonesian, Tamil, and Pashto Southern, and they have a variety of different schooling backgrounds. Many of the students attended the school the previous year, but a few students were new.

To launch the task, I used realia, real objects used as teaching aids, to provide students with a concrete representation of the information. Jars, bags, and straws are probably familiar objects; however, the English names might be new to some students.

Before students began working on the task, I asked: “How might you show your thinking so other students can understand your ideas?” Student responses included drawing pictures, using Unifix cubes, and writing equations. Many students began counting out cubes or drawing tally marks to represent the straws. I watched and listened to students as they worked.

Uncovering Student Assets

A multilingual learner new to our school had drawn a series of ovals on her paper (see the first image in this post). When I asked her how she was thinking about the problem, she said “straws” and pointed to her drawing. She then went up to the front of the room and brought the jar and bag of straws to her table. The audio file captures how this student engaged with the task of determining the total number of straws.

For this student, pencil and paper did not provide an avenue for her to leverage her assets; however, concrete objects did give her a way to reason through the task. She counted on from 24 and made a rote counting error that resulted in her answer being 1 more than the actual number of straws. Had I looked only at her written response, I wouldn’t have learned that she understands number as a composite unit. Had I not listened to her counting, I would not have learned that she knows many number names in English. In this instance, realia provided a means for the student to make sense of the task. As she thought through her solution, she realized she didn’t need to start counting at 1, but could instead count on from one of the known quantities. Through listening to and interacting with her while she was engaging in the task, I was able to learn about her many strengths and determine how she could leverage those strengths to make sense of the task.

Another student used Unifix cubes to represent the straws and wrote the equation 24 + 30 = 55. His answer, like the student above, was 1 more than the actual number of straws. When I looked at his representation of the task, I noticed the quantity 24 was organized into two groups of ten and four more cubes; however, the quantity 30 did not have grouping of tens.

I said to him, “I noticed that you showed 24 by making groups of ten and some more. How might you use groups of ten to help you find how many there are altogether?” This question was enough to prompt him to draw on what he knows about place value. He quickly reorganized the train of 30 cubes into three groups of ten. He then made a coordinated count of tens and ones to find the total of 54. Had I looked only at the equation he wrote, I would not have learned that he understands that numbers can be organized into groups of tens and ones, and that counting by tens and ones results in a total quantity.

Throughout the class, students used different approaches to reason through the task.  Some students made sense of the problem using concrete materials (straws, cubes), others used drawings that represented concrete objects, and some used numbers, words, and symbols. But all students were able to draw on their strengths in ways that made sense to them, which allowed for moving closer to grade-level understanding of place value. Though these examples highlighted second-grade multilingual learners solving a task involving addition, students from all backgrounds—in every grade level—have assets that can be leveraged through providing multiple avenues to reason through tasks in all areas of mathematics.

Multiple Avenues to Reason Through a Task

Concrete

(Physical objects that can be acted upon)

Pictorial

(Visual representations of concrete objects)

Abstract

(Numbers, notation, and mathematical symbols)